Estimate sums and differences of whole numbers
Key Notes :
| 🎇What is Estimation? |
Estimation: The process of finding an approximate value that is close to the actual value, often by rounding numbers.
- Purpose: Estimation helps make complex calculations simpler and quicker, especially when an exact answer is not necessary.
- Example: If you estimate the sum of 47 + 52, you might round them to 50 + 50 = 100.
| 🎁 When to Use Estimation |
Real-Life Situations: Estimation is useful when:
- Shopping and wanting to quickly determine the total cost.
- Planning a budget or making predictions.
- Checking the reasonableness of an answer without needing exact numbers.
| 🧨Steps for Estimating Sums and Differences |
Round the Numbers:
- Step 1: Identify the place value to which you will round (usually the nearest ten, hundred, or thousand).
- Step 2: Round each number to that place value.
- Example: To estimate 456+378, round each number to the nearest hundred: 456 rounds to 500, and 378 rounds to 400.
| 🧨Perform the Operation: |
Addition: Add the rounded numbers.
- Example: 500+400=900
Subtraction: Subtract the rounded numbers.
- Example: For 456−378, after rounding to the nearest hundred, 500−400=100
Compare with the Exact Answer (Optional):
- After finding the estimated sum or difference, you can calculate the exact answer and compare to see how close your estimate is.
- Example: 456+378=834 (exact), compared to the estimate of 900.
| 🎁 Rounding Rules |
Round Up:
- If the digit to the right of the place you’re rounding to is 5 or more, round up.
- Example: 76 rounds to 80 (nearest ten).
Round Down:
- If the digit to the right is less than 5, round down.
- Example: 42 rounds to 40 (nearest ten).
| Estimation Techniques |
Front-End Estimation:
- Focuses on the leftmost digits of the numbers (the “front”).
- Example: 435+289 → estimate using 400 and 200 to get 600.
Clustering:
- Used when numbers in a set are close in value. Round them to the same value for a quicker estimate.
- Example: 48,52,51 → round each to 50, then estimate 50+50+50=150
Compatible Numbers:
- Adjust numbers slightly to make mental math easier.
- Example: For 299+502, round to 300 and 500, then add 300+500=800
| 🎃 Importance of Estimation |
- Checking Work: Estimation allows you to quickly check if an answer is reasonable.
- Simplifying Complex Problems: It can make complex arithmetic easier by breaking it down into simpler steps.
- Building Number Sense: Helps develop an intuitive understanding of numbers and their relationships.
Learn with an example
Estimate the sum by rounding each number to the nearest thousand and then adding.
6,497 + 2,598
The sum is approximately____________ .
Round each number to the nearest thousand.
| 6,497 | + | 2,598 | = | ? |
| 6,000 | + | 3,000 | = | ? |
Now add:
| 6,000 | + | 3,000 | = | 9,000 |
The sum is about 9,000.
Estimate the sum by rounding each number to the nearest thousand and then adding.
4,033 + 2,804
The sum is approximately______________.
Round each number to the nearest thousand.
| 4,033 | + | 2,804 | = | ? |
| 4,000 | + | 3,000 | = | ? |
Now add:
| 4,000 | + | 3,000 | = | 7,000 |
The sum is about 7,000.
Estimate the sum by rounding each number to the nearest thousand and then adding.
6,281 + 8,412
The sum is approximately____________
Round each number to the nearest thousand .
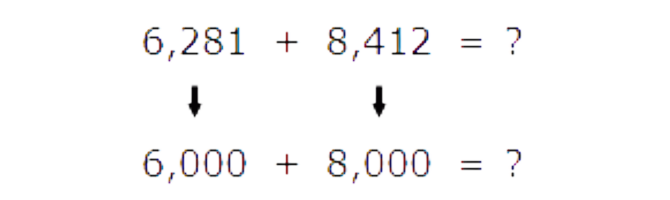
Now add :
6,000 + 8000 = 14,000
The sum is about 14,000.
Let’s practice!

