Multiply 2-digit numbers by 3-digit numbers
Key notes :
| ⭐ Key Points: |
- Multiplication of large numbers is done step by step.
- First, multiply the ones digit of the 2-digit number with the 3-digit number.
- Next, multiply the tens digit of the 2-digit number with the 3-digit number (remember to place a zero at the ones place).
- Add both results to get the final product.
| 🔹 Example 1: |
Multiply 46 × 325
Step 1: Multiply 325 × 6 (ones place of 46) 325×6=1950325 \times 6 = 1950325×6=1950
Step 2: Multiply 325 × 40 (tens place of 46, so add one zero) 325×40=13000325 \times 40 = 13000325×40=13000
Step 3: Add both results 1950+13000=149501950 + 13000 = 149501950+13000=14950
✅ Final Answer: 46 × 325 = 14,950
| 🔹 Example 2: |
Multiply 78 × 214
Step 1: Multiply 214 × 8 = 1712
Step 2: Multiply 214 × 70 = 14980
Step 3: Add 1712 + 14980 = 16692
✅ Final Answer: 78 × 214 = 16,692
| ✏️ Practice Problems: |
- 32 × 143 = ?
- 57 × 324 = ?
- 85 × 216 = ?
- 49 × 305 = ?
| 📌 Important Tips: |
- Always write numbers neatly in place value columns (ones, tens, hundreds, etc.).
- Don’t forget to add a zero when multiplying with the tens place.
- Double-check your addition at the end.
Learn with an example
Multiply:
561 x 17 =
Multiply the ones. Remember to carry over .
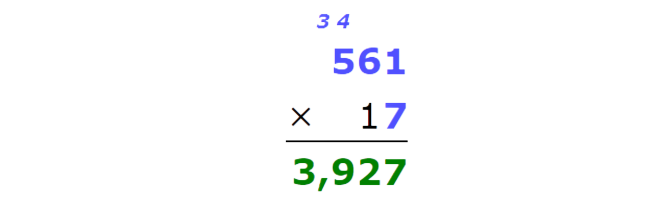
Multiply the tens.
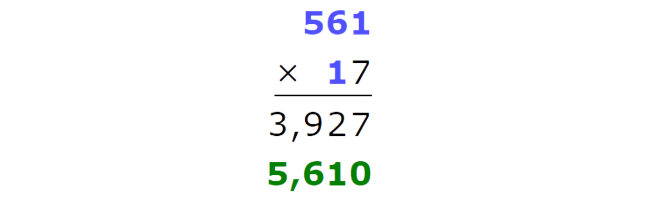
Now add the results.
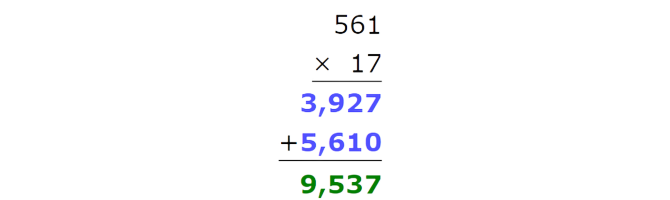
The product is 9,537.
Multiply:
544 x 94 =
Multiply the ones. Remember to carry over.
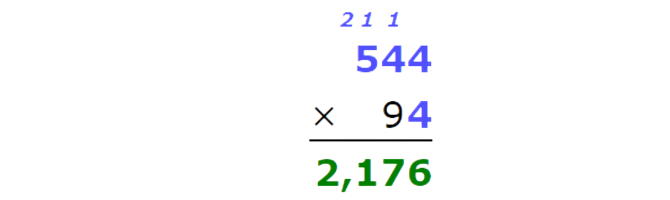
Multiply the tens. Remember to carry over.
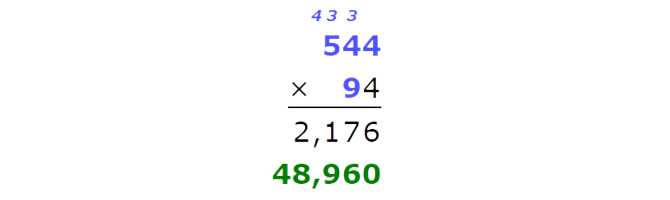
Now add the results.
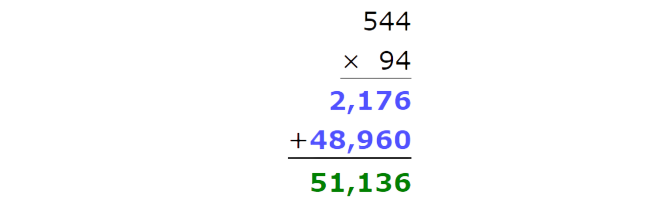
The product is 51,136.
Multiply:
328 x 84 =
Multiply the ones. Remember to carry over.
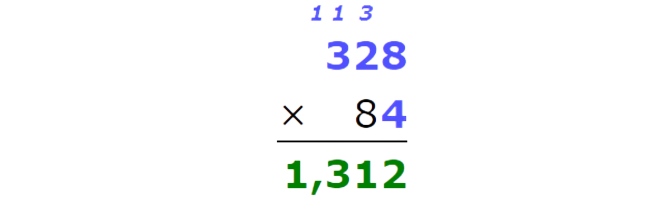
Multiply the tens. Remember to carry over.
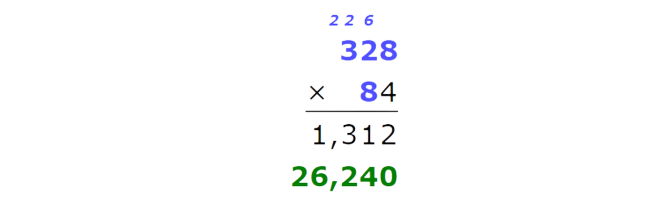
Now add the results.
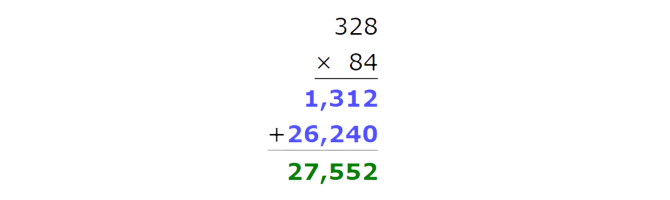
The product is 27,552.

Let’s practice!

