Compare decimals on number lines
key notes :
Comparing Decimals
Comparing decimals means finding out the larger and the smaller decimal number in a given set of numbers. Decimal numbers can be compared in the same way as we compare other numbers. However, we need to remember that the digits that are placed after the decimal point also need to be considered. These digits have place values starting from tenths, followed by hundredths, then thousandths, and so on. Let us learn more about comparing decimals in this article.
What is Comparing Decimals?
Comparing decimals is similar to comparing other whole numbers in which we start comparing the digits with the greatest place value. We place the given decimal numbers in a place value chart and start the comparison. If the digits on the greatest place value are the same, we move on to the digits in the next place to the right. We keep comparing digits until we reach the digits that are different. Let us understand this with the help of the following example.
Example: Compare 0.64 and 0.362
Solution:
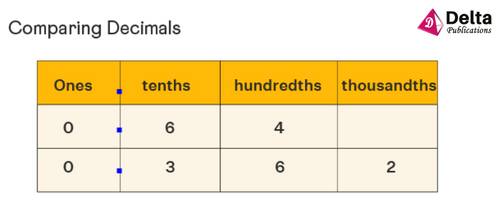
- Step 1: Compare the whole number part, which is the ones digit. If the numbers are the same, go to the next step. In this case, the ones digits has 0 in both the numbers. So, we move on to the next place to the right.
- Step 2: Compare the tenths place, which is the place to the right of the decimal point. When we compare the value in the tenths place, we see that 6 is greater than 3. At this step itself, we get to know that 0.64 is greater than 0.362. Therefore, we do not need to move on to the hundredths digit for further comparison.
- Step 3: Hence, we conclude that 0.64 > 0.362
Comparing Decimals and Fractions
When we need to compare decimals and fractions, we first convert the given fraction to a decimal number and then compare the numbers using the same procedure.
Example: Compare 3/4 and 0.728
Solution: First, let us convert 3/4 to a decimal number by dividing 3 by 4. So, 3 ÷ 4 = 0.75. Now, we have both the numbers in the decimal form. So, let us compare 0.75 and 0.728 using the method given above.
- Step 1: Compare the whole number part, which is the ones digit. In this case, the ones digits has 0 in both the numbers. So, we will move on to the next place value to the right.
- Step 2: Compare the tenths place, which is the first place to the right of the decimal point. When we compare the value on the tenths digit, we see that both the numbers have 7. So we move on to the hundredths place.
- Step 3: Compare the hundredths place. Now, when we compare the value at the hundredths place, we see that 5 is greater than 2. At this step, we get to know that 0.75 is greater than 0.728. Therefore, we do not need to move on to the thousandths digit for further comparison.
- Step 3: Hence, we conclude that 0.75 > 0.728 which means 3/4 > 0.728
Comparing Decimals on a Number Line
When we compare decimals on a number line, we follow the basic rule of the number line which says that, as we move to the right the value of the numbers increases. For example, if we need to compare 6.5 and 6.7, we mark the decimal numbers on the number line in such a way that both the numbers are included.
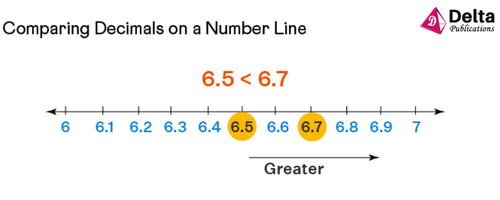
We need to focus between 6 and 7 because both the given numbers lie between 6 and 7. We mark 6 at the left end and 7 at the right end. Then, we mark all the numbers in between, to scale, writing 6.5 midway between 6 and 7. After marking the other tenths, we see that 6.7 comes to the right side of 6.5, therefore 6.5 < 6.7. Hence, it be concluded that 6.5 < 6.7 because 6.7 comes to the right of 6.5 on the number line.
Comparing Decimals to Hundredths place
We have already seen that we compare decimal numbers starting from the whole number part and then we move on to the digits given after the decimal point. Let us see how to compare decimals to the hundredths place.
Example: Compare 8.362 and 8.391 to find the greater number.
Solution: Let us follow the same steps as shown above.
- Step 1: Compare the whole number part. In this case, the whole number part has 8 in both the numbers. So, we will move on to the next place value.
- Step 2: Compare the tenths place, which is the first place to the right of the decimal point. When we compare the value on the tenths digit, we see that both the numbers have 3. At this point, we move on to the hundredths place.
- Step 3: Compare the hundredths place. Now, when we compare the value at the hundredths place, we see that 9 is greater than 6. So, we get to know that 8.391 is greater than 8.362. Therefore, we do not need to move on to the thousandths digit for further comparison.
- Step 3: Hence, we conclude that 8.362 < 8.391
Learn with an example
Graph 0.2 and 0.1 on the number line.

Which number is closer to 0.0?
- 0.2
- 0.1
Graph 0.2.
Find 0.2 on the number line and graph the point.

Graph 0.1.
Find 0.1 on the number line and graph the point.
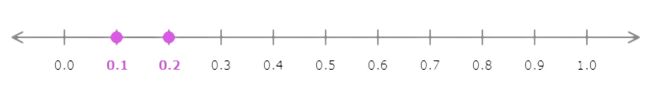
Compare 0.2 and 0.1.
0.1 is closer to 0.0.
Graph 0.5 and 0.7 on the number line.

Which number is closer to 1.0?
- 0.5
- 0.7
Graph 0.5.
Find 0.5 on the number line and graph the point.

Graph 0.7.
Find 0.7 on the number line and graph the point.

Compare 0.5 and 0.7.
0.7 is closer to 1.0.
Graph 0.5 and 0.3 on the number line.

Which number is closer to 0.0?
- 0.5
- 0.3
Graph 0.5.
Find 0.5 on the number line and graph the point.

Graph 0.3.
Find 0.3 on the number line and graph the point.

Compare 0.5 and 0.3.
0.3 is closer to 0.0.
Let’s practice!

