Compare fractions

Key Notes :

⭐ Understand the Fraction Parts

  • Numerator ➡️ Top number (how many parts) 🔢
  • Denominator ➡️ Bottom number (total parts) 🧩
  • Bigger denominator = smaller pieces 🍪🍪🍪

🎨 Compare Fractions with Same Denominator

👉 When denominators are the same,
compare numerators.

  • Example: 3/8 < 5/8 because 5 pieces are more! 🎉

📌 Same bottom ➡️ Compare top! 🟦🟩

🎨 Compare Fractions with Same Numerator

👉 When numerators are the same,
compare denominators.

  • Example: 1/4 > 1/8 because 1 out of 4 is a bigger piece than 1 out of 8! 🍕🍕

📌 Same top ➡️ Compare bottom! 🟨🟥

🌟 Use Equivalent Fractions

👉 Turn fractions into equivalent forms to compare.

  • Example: Compare 2/3 and 3/5
    • 2/3 = 10/15
    • 3/5 = 9/15
      So, 2/3 > 3/5 🎯

💡 Multiply numerator and denominator by the same number 🔄

📊 Use the LCM method (Common Denominator)

👉 Change both fractions to have the same denominator.

  • Example: 3/4 and 2/3
    • LCM of 4 and 3 = 12
    • 3/4 = 9/12
    • 2/3 = 8/12
      So, 3/4 > 2/3 🎉

🍕 Use Visual Models

  • Fraction strips 🎨
  • Pie models 🍩
  • Number lines 📏
    📌 Helps to see which fraction is bigger.

🔢 Compare Using Decimal Values

👉 Convert fractions to decimals when needed.

  • Example: 1/2 = 0.5
  • 3/4 = 0.75
    So, 3/4 > 1/2 📈

🎯 Use Benchmarks (0, 1/2, 1)

👉 Check whether the fraction is

  • Less than ½ 🍃
  • Equal to ½ ⚖️
  • Greater than ½ 🌟

Example: 7/12 > 1/2 because 7 is more than half of 12.

🎉 Use Symbols Correctly

  • < means smaller
  • > means greater
  • = means equal

📌 Example: 5/6 > 3/6 ✨

🌟 Practice Makes Perfect!

✔ Draw models
✔ Convert
✔ Compare visually and mathematically
✔ Use real-life examples like pizza slices 🍕, chocolate bars 🍫

Learn with an example

Which fraction is greater?

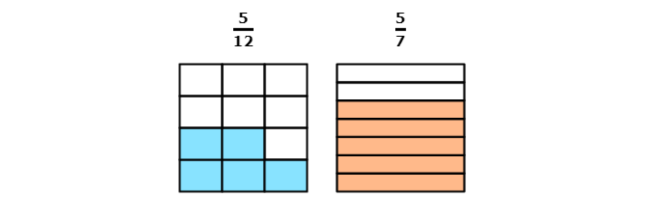
  • 5/12
  • 5/7

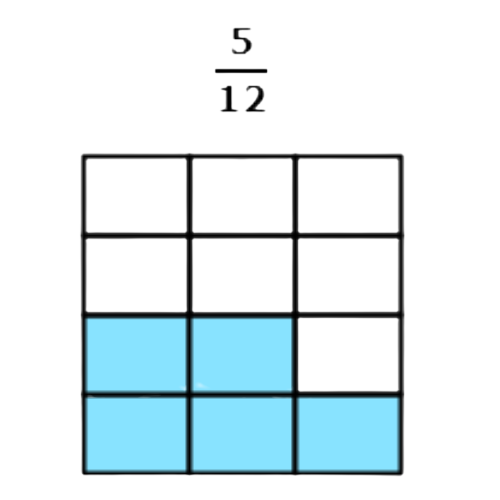
5 out of 12 equal parts are coloured.

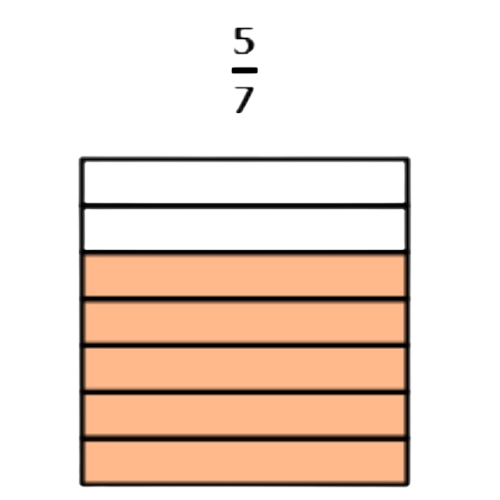
5 out of 7 equal parts are coloured.

Both shapes have 5 coloured parts, but the parts in the second shape are larger. This is because the second shape is only sliced into 7 parts, instead of 12.

So, more of the second shape is coloured.

5/7  is greater than  5/12 .

Which fraction is greater?

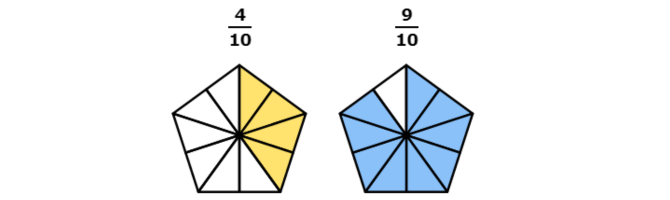
  • 4/10
  • 9/10

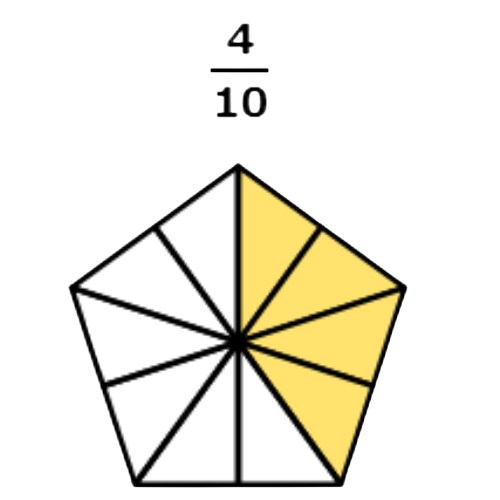
4 out of 10 equal parts are coloured.

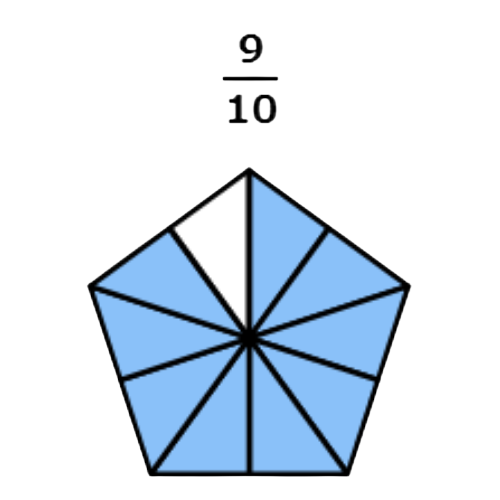
9 out of 10 equal parts are coloured.

Both shapes have 10 equal parts and are the same size. So, the parts in the first shape are the same size as the parts in the second shape.

When parts are the same size, 9 parts is more than 4 parts. So, more of the second shape is coloured.

9/10  is greater than 4/10 .

Which fraction is greater?

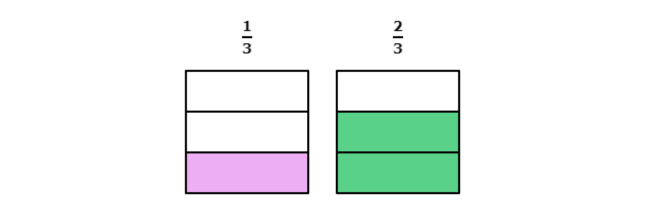
  • 1/3
  • 2/3

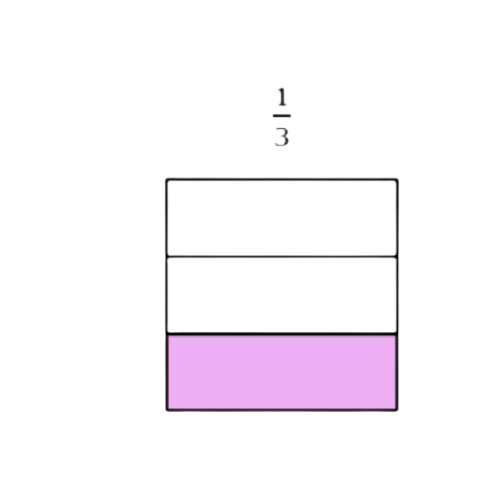
1 out of 3 equal parts are coloured.

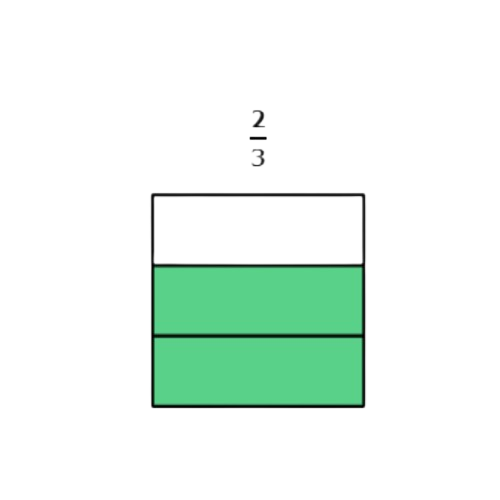
2 out of 3 equal parts are coloured.

Both shapes have 3 equal parts and are the same size. So, the parts in the first shape are the same size as the parts in the second shape.

When parts are the same size, 2 parts is more than 1 part. So, more of the second shape is coloured.

2/3  is greater than 1/3 .

Let’s try some problems!✍️