Put fractions in order
Key Notes :
🔢 Understand the Parts of a Fraction
- Numerator ➡️ Top number (how many parts).
- Denominator ➡️ Bottom number (total parts).
📌 The bigger the denominator, the smaller each part! 🍕➡️🍰
🔄 Use Common Denominators
To compare or order fractions:
- Make denominators same ✔️
- Change each fraction to an equivalent fraction.
🧮 Example:
1/2 = 3/6
2/3 = 4/6
🔍 Compare Using Common Denominators
Once denominators are equal:
- Compare numerators
- Bigger numerator = bigger fraction 📈
- Smaller numerator = smaller fraction 📉
✨ Example:
3/6 < 4/6
📏 Use Number Line to Order Fractions
- Place fractions on a number line 0 ➡️ 1
- The fraction farther right ➡️ greater
- The fraction farther left ➡️ smaller
📍 0 ———— 1/4 ———— 1/2 ———— 3/4 ———— 1
🍰 Compare Fractions with Same Numerator
If numerator same, compare denominators:
- Smaller denominator = larger fraction
- Bigger denominator = smaller fraction
🎉 Example:
3/5<3/4
because 1/4 pieces are bigger!
🔢 Convert Mixed Numbers if Needed
For ordering mixed numbers:
- Compare whole numbers first
- If whole numbers same, compare fraction parts
🍎 Example:
3 ½ > 3 ¼
⭐ Use Benchmarks (0, 1/2, 1)
- Compare fractions with ½ or 1 to understand size
🤔 Example:
Is 3/8 < 1/2? Yes, because 3/8 is less than 4/8.
🎉 Order Fractions from Least to Greatest or Greatest to Least
- After comparing, arrange in correct order
- Always check your conversions ✔️
🌈 FINAL TIP
👉 Practice comparing fractions using real objects: pizza 🍕, chocolate 🍫, cakes 🎂, or diagrams 📊!
Learn with an example
🙂Put these fractions in order from largest to smallest.
- 6/11
- 6/8
- 6/9
These shapes show the fractions from largest to smallest:
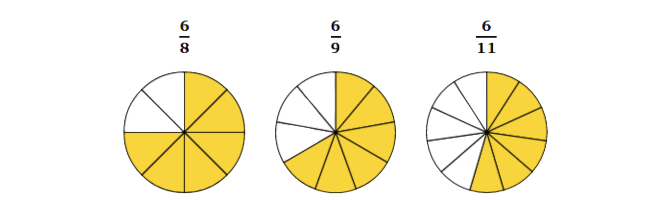
Each shape has 6 parts shaded. Notice that each shape has smaller parts than the previous shape. The total shaded part of each shape is smaller than in the previous shape.
The fractions in order from largest to smallest are:
- 6/8
- 6/9
- 6/11
🙂 Put these fractions in order from smallest to largest.
- 4/10
- 2/10
- 3/10
- 9/10
These shapes show the fractions from smallest to largest:
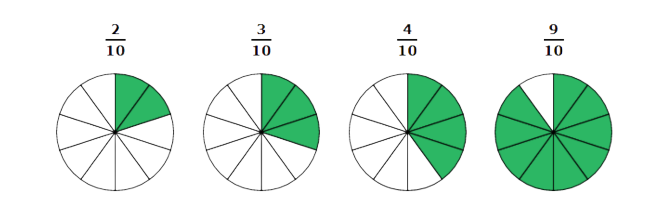
Each shape has 10 parts. Notice how each shape has more parts shaded than the previous shape.
The fractions in order from smallest to largest are:
- 2/10
- 3/10
- 4/10
- 9/10
🙂 Put these fractions in order from smallest to largest.
- 6/11
- 6/10
- 6/7
- 6/8
These shapes show the fractions from smallest to largest:
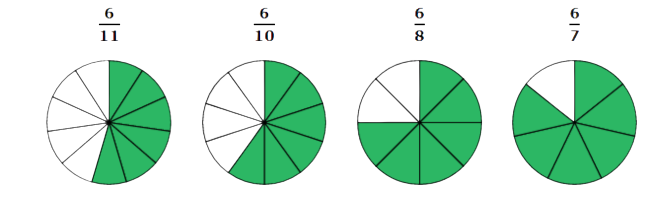
Each shape has 6 parts shaded. Notice that each shape has larger parts than the previous shape. The total shaded part of each shape is larger than in the previous shape.
The fractions in order from smallest to largest are:
- 6/11
- 6/10
- 6/8
- 6/7
Let’s try some problems!

