Use Venn diagrams to solve problems
Key Notes :
1. What is a Venn Diagram?
- A Venn diagram is a graphical tool used to show the relationships between different sets of items or groups.
- It consists of overlapping circles. Each circle represents a set, and the area where the circles overlap shows the common elements between the sets.
2. How Venn Diagrams Work
- Non-overlapping circles: Represent sets that have no common elements.
- Overlapping circles: Show the common elements between the sets in the overlapping area.
- Entire circles: Represent all the elements of a set, whether or not they share anything with other sets.
3. Basic Components
- Universal set: The set of all elements being considered. It is usually represented by a rectangle surrounding the circles.
- Sets: The circles represent sets of items. Each circle contains elements that belong to that specific set.
- Intersection: The overlapping region where two or more sets share common elements.
- Union: All the elements in the Venn diagram (elements in any of the circles or both).
- Difference: Elements that belong to one set but not the other.
Learn with an example
1) 4 of the students in Charlotte’s class have a jacket with a hood and 6 have a jacket with buttons. 3 students have a jacket with both a hood and buttons.
How many students have a jacket with buttons but not a hood?
____ students
Make a Venn diagram to solve the problem.
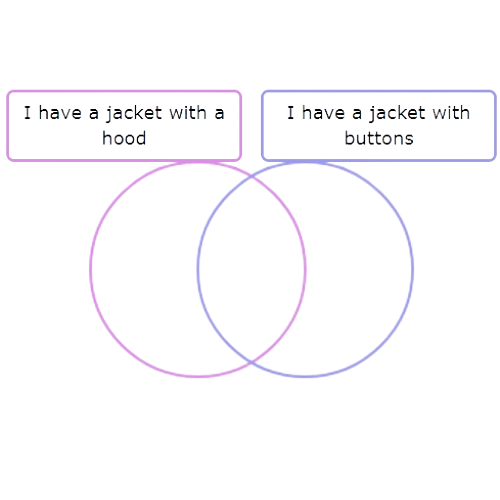
3 students have a jacket with both a hood and buttons. Put 3 dots in the area that is in both circles.
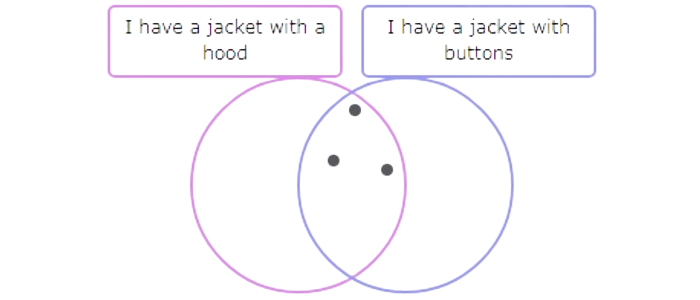
Now add dots to the other two areas until there are 4 dots in the “I have a jacket with a hood” circle and 6 dots in the “I have a jacket with buttons” circle.
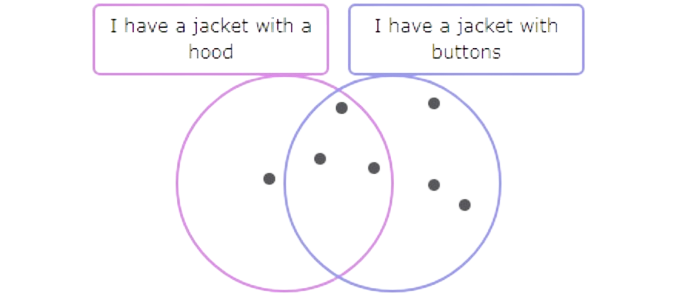
Count the dots that are in the “I have a jacket with buttons” circle but are not in the “I have a jacket with a hood” circle. There are 3 dots.
3 students have a jacket with buttons but not a hood.
2) 4 of the children in Carrie’s class have an orange marble. 3 children have a red marble, and 2 children have both an orange marble and a red marble.
How many children have a red marble but not an orange marble?
____ children
Make a Venn diagram to solve the problem.
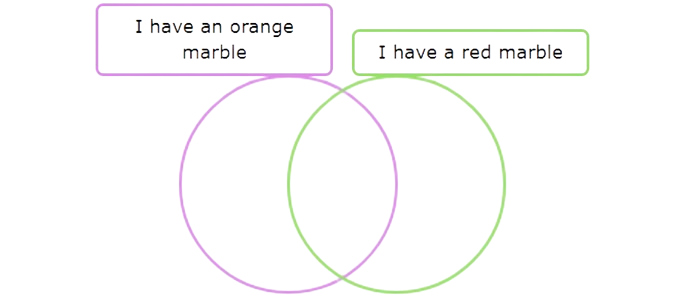
2 children have both an orange marble and a red marble. Put 2 dots in the area that is in both circles.
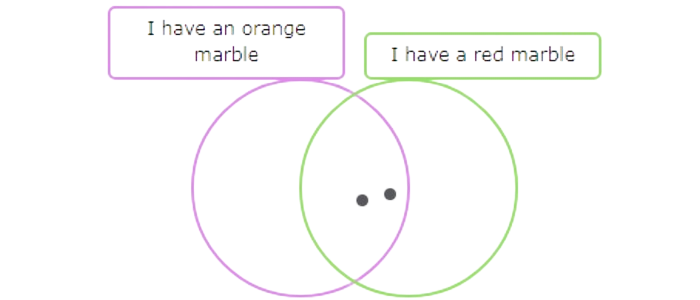
Now add dots to the other two areas until there are 4 dots in the “I have an orange marble” circle and 3 dots in the “I have a red marble” circle.
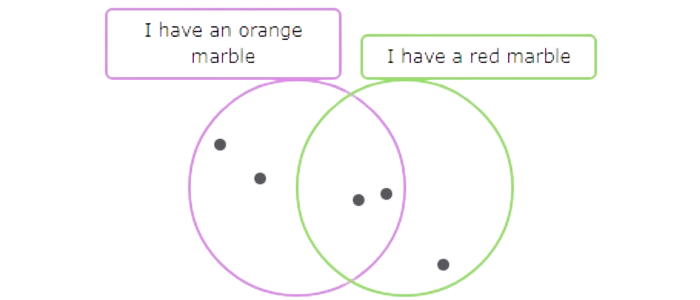
Count the dots that are in the “I have a red marble” circle but are not in the “I have an orange marble” circle. There is 1 dot.
1 child has a red marble but not an orange marble.
3) 7 of the people in Levi’s flat building like leopards and 7 like jaguars. 5 people like both leopards and jaguars.
How many people like leopards or jaguars or both?
_____ people
Make a Venn diagram to solve the problem.
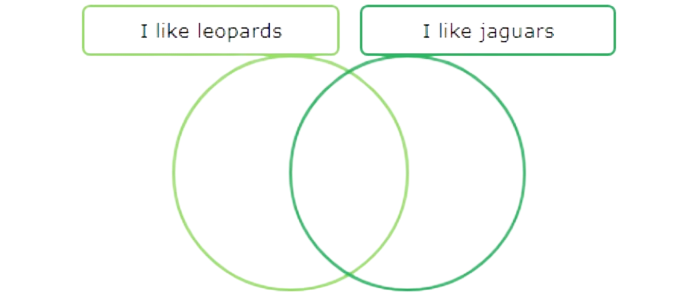
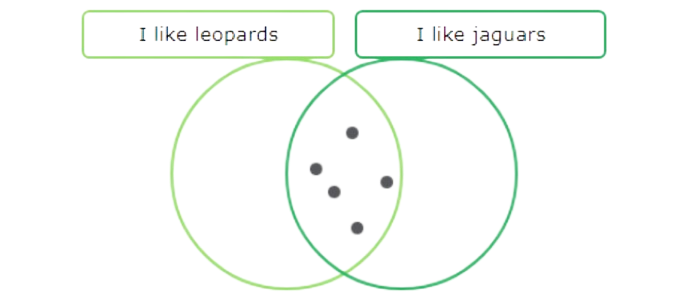
5 people like both leopards and jaguars. Put 5 dots in the area that is in both circles.
Now add dots to the other two areas until there are 7 dots in the “I like leopards” circle and 7 dots in the “I like jaguars” circle.
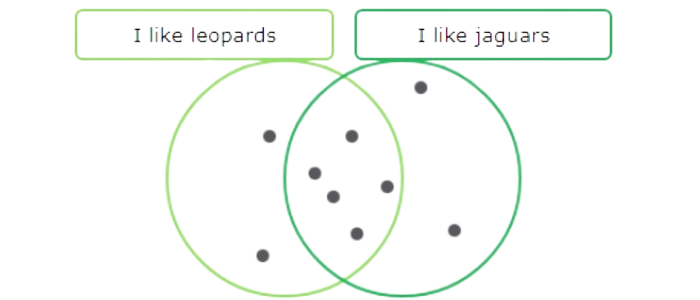
Count the total number of dots in the diagram. There are 9 dots.
9 people like leopards or jaguars or both.
Let’s practice!🖊️

