Combinations
Key notes :
Definition of Combinations
- A combination is a way of selecting items from a group where the order does not matter.
- Example: Choosing 2 fruits from {Apple, Banana, Orange} → {Apple, Banana}, {Apple, Orange}, {Banana, Orange}.
Difference Between Combinations and Permutations
- Combinations: Order does not matter. (Example: Choosing 2 team members from a group).
- Permutations: Order does matter. (Example: Assigning 1st and 2nd place in a race).
Formula for Combinations
- The formula for finding the number of ways to choose r items from n items is:
C(n,r) = n! / r!(n−r)!
- Example: Choosing 2 students from a group of 4 →
C(4,2) = 4! / 2!(4−2)! = 4×3 / 2 × 1 = 6
Examples of Combinations in Daily Life
- Choosing a group of friends for a trip.
- Selecting different toppings for a pizza.
- Forming teams in a class project.
Key Concept: Order Does Not Matter
- If you select A and B, it is the same as selecting B and A.
- This makes combinations different from arrangements.
Learn with an example
🌀 Dwayne wants to get a sandwich from the deli for lunch. He can pick a roast beef, turkey, or tuna sandwich. The bread choices are white or multi-grain.
How many different combinations can Dwayne pick from?
_______ combinations
There are 3 sandwich choices and 2 bread choices. Multiply to find the number of possible combinations:
3 × 2 = 6
There are 6 combinations.
You could also make a list of all the combinations.
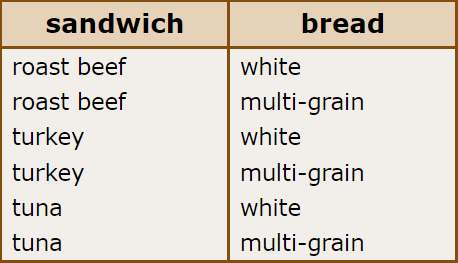
Now count the combinations. There are 6 combinations.
🌀Riley is ordering a birthday cake for a friend. The bakery makes carrot, chocolate, and lemon flavoured cakes. Each flavour of cake can come with yellow or green frosting.
How many different combinations can Riley choose from?
________ combinations
There are 3 flavour choices and 2 frosting choices. Multiply to find the number of possible combinations:
3 × 2 = 6
There are 6 combinations.
You could also make a list of all the combinations.
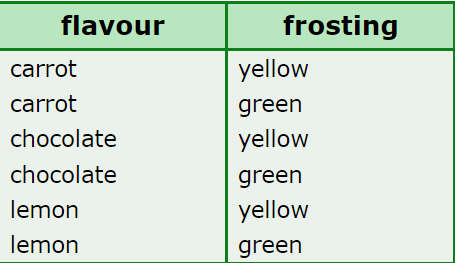
Now count the combinations. There are 6 combinations.
🌀 Krysta is going out for a pasta dinner. She can choose fettuccine, shell, or macaroni pasta, and she can have garlic, cream, or pesto sauce.
How many different combinations can Krysta have for dinner?
________ combinations
There are 3 pasta choices and 3 sauce choices. Multiply to find the number of possible combinations:
3 × 3 = 9
There are 9 combinations.
You could also make a list of all the combinations.
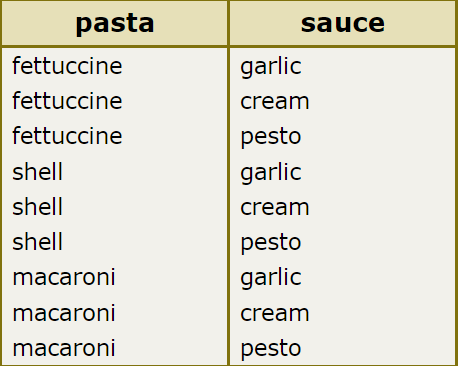
Now count the combinations. There are 9 combinations.
Let’s practice!🖊️

