Area and perimeter: word problems
Key Notes :
Area Word Problems:
- Identifying Shapes: Recognize the shape described in the problem (e.g., rectangle, square, irregular shape).

Calculating Area:
- Rectangles and Squares: Use the formula Area=length×width.
- Irregular Shapes: Break down the shape into simpler rectangles or squares, calculate their areas, and then sum them up.

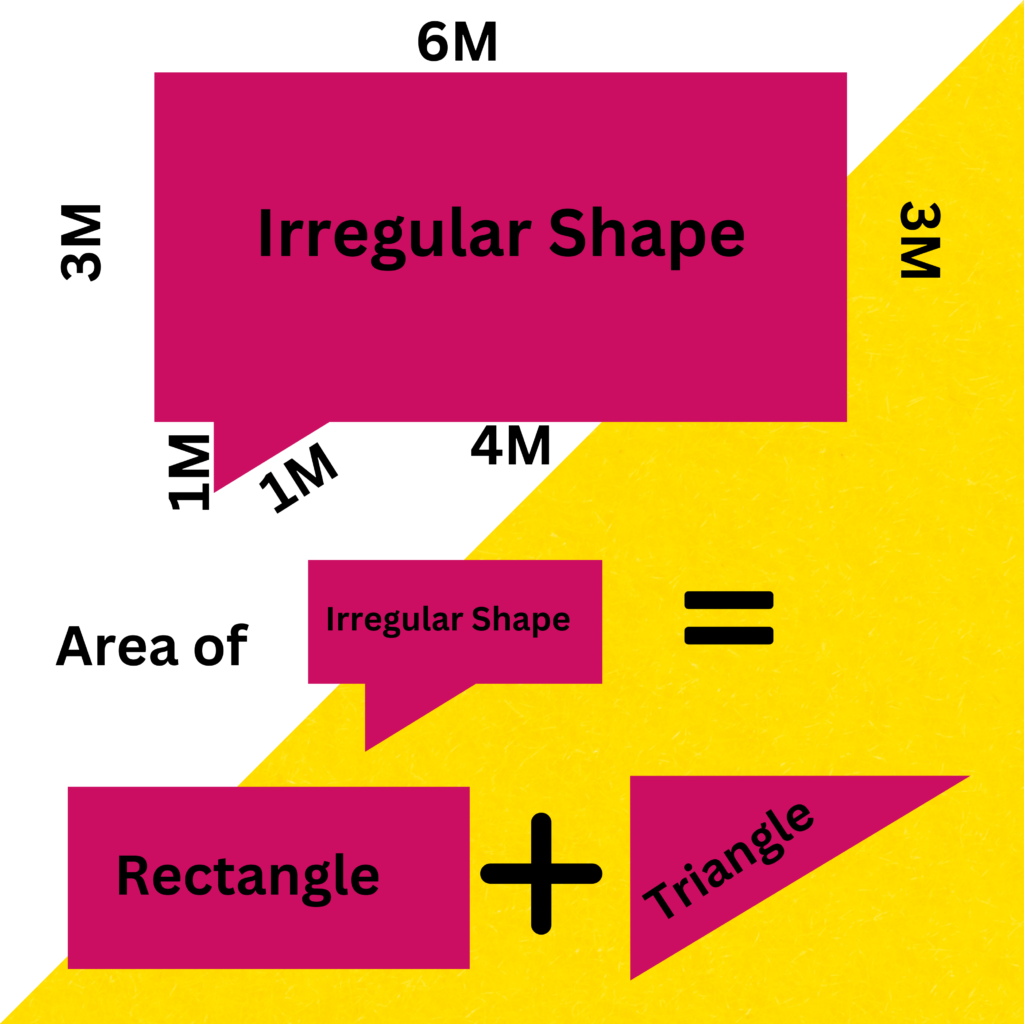
Perimeter Word Problems:
- Identifying Shapes: Understand the shape described (e.g., rectangle, square, closed irregular figure).

Calculating Perimeter:
- Rectangles and Squares: Use the formula Perimeter=2×(length+width)
- Irregular Shapes: Add the lengths of all sides of the shape.

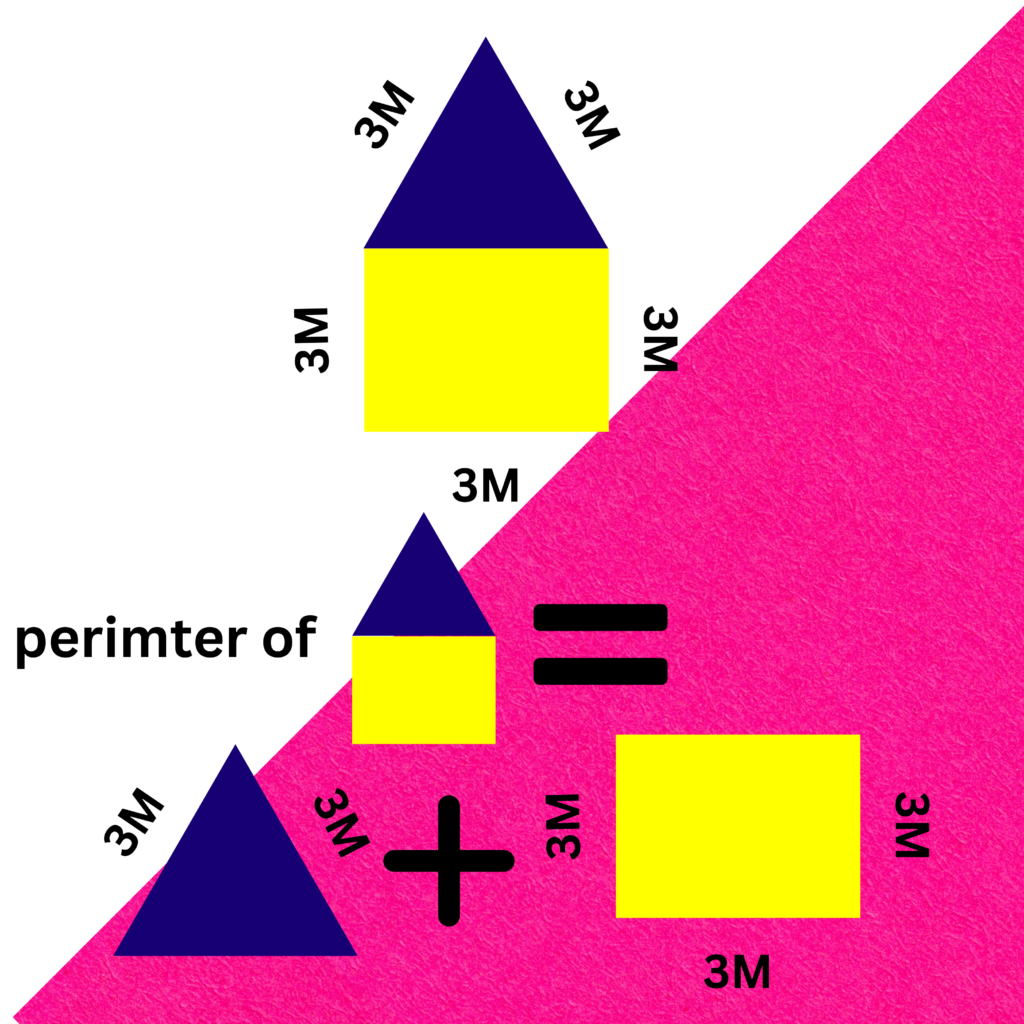
Problem-Solving Strategies:
- Read Carefully: Understand the problem statement and identify what information is provided and what is needed.
- Draw Diagrams: Sketch the shape described in the problem, especially when dealing with irregular shapes.
- Label: Label dimensions clearly on the diagram to avoid confusion.
- Compute Correctly: Use the appropriate formulas for area and perimeter based on the given shape.
- Check Units: Always check that the units in the final answer are appropriate and consistent with the problem context.
Learn with an example
▶️ A square market has a perimeter of 28 metres. How long is each side of the market?
___ metres
A square has 4 equal sides.
Divide the perimeter by 4 to find the length of each side:
28 ÷ 4 = 7
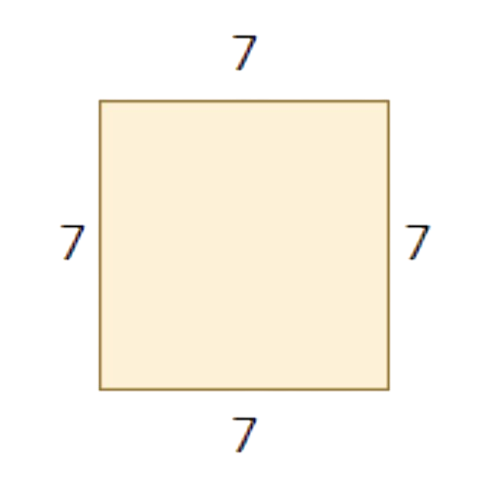
Each side is 7 metres long.
▶️ A square plastic tarp has a perimeter of 60 metres. How long is each side?
______ metres
A square has 4 equal sides.
Divide the perimeter by 4 to find the length of each side:
60 ÷ 4 = 15
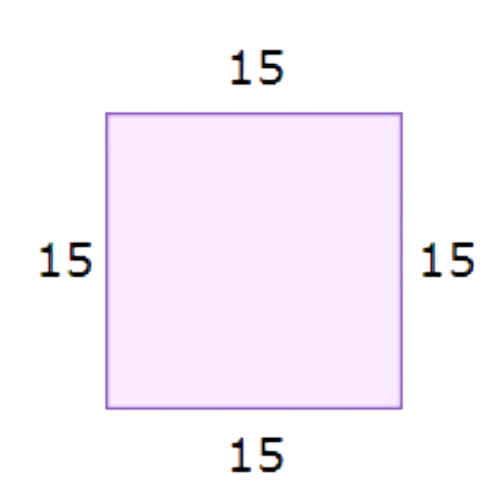
Each side is 15 metres long.
▶️ A rectangular vegetable patch is 3 metres wide and 5 metres long. What is its area?
______ square metres
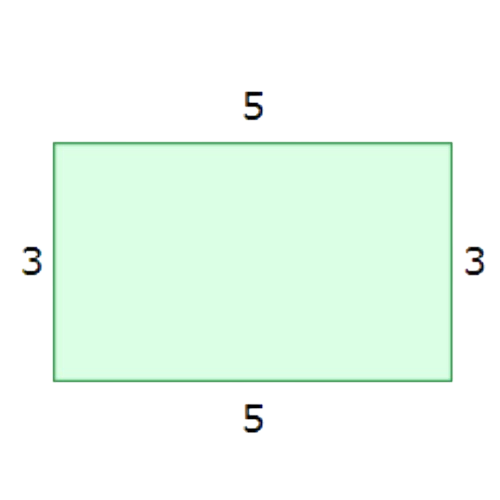
Multiply the length times the width:
3 × 5 = 15
The area is 15 square metres.
Let’s practice!🖊️

